Расчет сварной главной балкиСтраница 6
![]() =18кН/см2 – расчетное сопротивление металла шва сварных соединений с угловыми швами принимаем по таблице 56 СНиП II-23–81* в зависимости от вида электродов.
=18кН/см2 – расчетное сопротивление металла шва сварных соединений с угловыми швами принимаем по таблице 56 СНиП II-23–81* в зависимости от вида электродов.
![]() см
см
В соответствии с видом сварки-ручная, пределом текучести стали
Ryx ≤ 430 мПа, tf=20 мм по таблице 38* принимаем kf= 7 мм.
Вид электродов, принимается в зависимости от марки стали и вида сварки, по таблице 55* СНиП II-23–81*. Сталь С255 материал для сварки электродом Э 42А.
Во избежание больших усадочных напряжений поясные швы следует устраивать сплошными, одинаковой толщины, используя ручную сварку.
Поясные швы, выполненные с полным проваром на всю толщину стенки, считаются равнопрочными со стенкой.
Расчет опорной части балки.
При шарнирном опирании сварных балок на нижележащие конструкции передача опорной реакции осуществляется через парные опорные ребра, плотно приваренные к нижнему поясу балки, или соединенные при помощи торцевого ребра жесткости (рисунок 16).
Размеры опорного ребра устанавливают из расчета на смятие его торцов:
![]() , (2.42)
, (2.42)
где ![]() - расчетное сопротивление смятию торцевой поверхности,
- расчетное сопротивление смятию торцевой поверхности,
принимаемое по таблице 52* СНиП II-23–81* в зависимости от временного сопротивления проката.Rp=327кН/м2 т. к. Ru=360 кН/м2
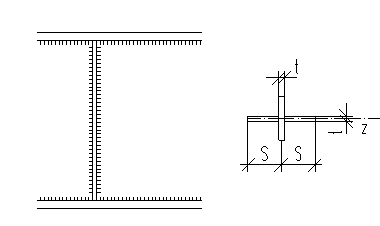
Рисунок 16 – К расчету опорных ребер.
![]() см
см![]() .
.
Обычно задаются шириной опорного ребра, а толщину определяют, исходя из требуемой площади смятия:
![]() , (2.43)
, (2.43)
где ![]() см.
см.
![]() см,
см,
принимаем td=12 мм.
Вследствие недостаточных размеров ребра опорный участок стенки может потерять устойчивость из своей плоскости, поэтому его рассчитывают на продольный изгиб как стойку с расчетной длиной, равной высоте стенки:
![]() , (2.44)
, (2.44)
где ![]() – коэффициент продольного изгиба, определяется в зависимости от гибкости стенки.
– коэффициент продольного изгиба, определяется в зависимости от гибкости стенки.
Гибкость стенки равна:
![]() (2.45)
(2.45)
![]() – радиус инерции сечения относительно оси z, равен:
– радиус инерции сечения относительно оси z, равен:
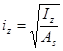 (2.46)
(2.46)
![]() – момент инерции сечения относительно оси z без учета момента инерции стенки, равен:
– момент инерции сечения относительно оси z без учета момента инерции стенки, равен:
![]() (2.47)
(2.47)
![]() см
см![]()
![]() – площадь условного крестового сечения, принятого в расчете, включающая опорные ребра и полосу стенки шириной S с каждой стороны ребра.
– площадь условного крестового сечения, принятого в расчете, включающая опорные ребра и полосу стенки шириной S с каждой стороны ребра.
Находим ширину полосы стенки:
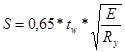 (2.48)
(2.48)
![]() см
см
Находим площадь сечения:
![]() (2.49)
(2.49)
![]() см
см![]()
Находим радиус инерции сечения:
![]() см
см
Находим гибкость стенки:
![]()
принимаем φ=0,9
![]() кн/см
кн/см![]()
16,9 < 24 кн/см![]()
условие выполняется.
Сопряжения отправочных марок
Навигация
- Главная
- Расчет состава тяжелого и легкого бетона
- Функциональные особенности материалов в интерьере
- Основания и фундаменты
- Полы
- Штукатурные работы
- Архитектурный стиль ампир
